積分 挑戦状 怪物を生み出す好奇心

質問

＜難問＞ (√cos2x)/sin(x+pi/4) を 0~pi/4 の範囲でxについて積分せよ。

＜難問＞(√cos2x)/sin(x+pi/4)を0~pi/4の範囲... - Yahoo!知恵袋

積分 ∫ [0,π/4] √(cos(2x))/sin(x+π/4) dx

回答

これは自力で完答するのは難しい問題ですね、何度か手順をなぞって考え方を追体験しておくと役立つかと思います。

この一問で様々な積分テクニックが詰め込まれてます。各々をガッツリ解説すると相当長くなってしまいますので、ステップを分けてさらっと進めさせていただきます。

STEP1：King Rule

まずはsin,cosの引数がまとまりがない状態なので、π/4までという積分区間を利用してKing Rule(Property)と呼ばれる必殺技を初手からぶちかまします。

するとそれぞれの引数でπ/2が現れますので、三角関数は90度回転で簡単になるなー、と発想が浮かぶかがポイント。

ルートをうまく使えば被積分関数が非常にコンパクトになっちゃいます。

STEP2：根号置換

ですがコンパクトだから簡単とは限らない。

この∫ [0,π/4] √(tan(t)) dt という積分、受験数学の積分ではメチャクチャハードな問題として有名なんです。

（この問題の解説はYouTubeにて「ヨビノリの今週の積分 #100」で紹介されてるため、そちらに任せてしまいたくなる……そっちもぜひ確認してみてくださいませ）

√(tan(t)) = u と、根号の式は丸ごと置換しましょう。

すると、dt = 2u/(1+u^4) du という、4次式が分母に来ます。もうヤバい雰囲気が察せられますね。

STEP3：BBB

せめて分子側が3次式だったら対数微分のタイプで楽なのですが、此度は観念して4次式 1+u^4 を因数分解しましょう。「複二次式」ですね、この因数分解１ステップだって知らないと独力で解くのは困難でしょうに、ここからさらにヘビーな計算が待ってます。

分母が無事にバラせて、∫ [0,1] 2u^2/{(u^2-√2 u +1)(u^2+√2 u +1)} du となったら4次の「部分分数分解」に取り掛かります。4元連立方程式……

これも慣れてくれば細かなテクニックもあるんですが割愛。

上手く分解できたら(1次式)/(2次式)となりますので、対数微分の形が使えるよう係数と定数部分を調整して、結果４項の積分へとバラせました。

STEP4：tan置換

対数の側は定積分で簡単に落とせるので、残った 1/(2次式) の処理にかかります。

分母の2次式は平方完成して二乗和の形を意識しながらtan置換します。

ここでまた難所、tan(θ)=√2 ±1 となるθって導けますか？ というハードルが現れます。

貼り付けた手書きの計算用紙に図形を載せておきました、二等辺三角形と外角・内角の関係を利用すれば tan(π/8)=√2 -1 が導ける方法も、知らないと「未知の角度α,βと置いて、定積分の後でtanの加法定理でまとめて〜」と論証が要求されます。手間！

FINAL：式のまとめ

そうこうしてようやく全ての定積分が解けました。後はとっ散らかった式を整頓しましょう。

logの中身もあらかじめ√2で約分しておくと、二重根号を考えず単に有理化するだけで済みますね。

結論：∫ [0,π/4] √(cos(2x))/sin(x+π/4) dx = log(√2 -1) +π/2

シンプルで美しくも不思議な答えが得られましたね。

ここで用いたいくつかの積分テクニックを武器として使えるようにしていれば、大概の問題は解けるようになると思います。

詳細な式は端折りましたがそれでも長くなってしまいました。

参考になれば幸いです。

返答

丁寧にありがとうございます！

最後に、この問題に部分積分を組み込みたいのですが、流石に無理ですかね？(笑)

返信

この問題に部分積分を組み込むのは思いつきませんでしたが、この問題を得るために部分積分が必要になるように、改造することはできちゃいました(笑)

難易度がヤバいなんてもんじゃ済まなくなりましたが、誰かをビビらせたりパズルとして楽しむ分には覿面かと。

∫ [0,π/4] sin(2x)/√(cos(2x)) log(tan(x/2 +π/8)) dx

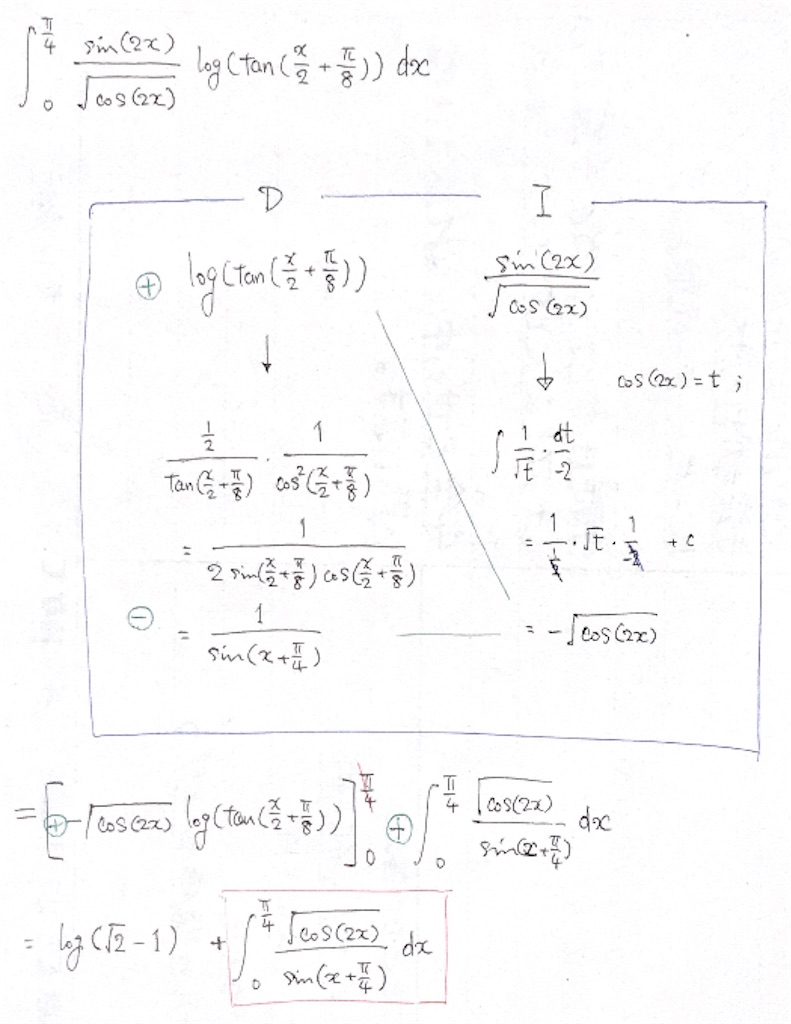
部分積分の微分側にも積分側にも、置換に倍角にとテクニックを要します。

無事に分離できてからが、さぁ今回のご質問だった積分の始まりですので、初見攻略だとまぁビビります。

おまけにこの部分積分で先に出てしまう定数 log(√2 -1)って、ご質問の積分の結果にも再度出てくるものなので、最後の答えもごちゃごちゃせずに済みます。

楽しい。

ご要望とはズレたかもしれませんがご参考までに……

怪物を生み出す好奇心

好奇心の生み出す怪物と言ったらメアリ・シェリーの「フランケンシュタイン」がパッと浮かんだが、

「作られる側からしたらたまったもんじゃない」といった切り口で描かれることが多いテーマ。

根拠のない誕生・存在の根の浅さに対する悲嘆とでも言うのか、「反出生主義」にも触れそうな嘆き。

もしくは、ハガレンのタッカーさんのキメラ練成など「人間の愚かさ・エゴイズム」寄りの舵取り。

けれど数学からすればその姿の方が極めて自然な状態で、それを醜い怪物のようだと思うのは人間の感性でそれを捉えているから……なのかもしれない。

「モンスターな数式・問題」という感想は、私たちの視点の方が穿った見方である可能性もある。

怪物は自分を産んでくれる好奇心を誘っている？

だけどこと数式の"難しさ"と言う怪物は、数学にもともと仕組まれていたもののようにも思われる。

そして先のとは真逆のイメージで悪魔召喚のように術者を唆し、

「オレを暴いてくれてありがとよ」と喜びの産声を上げて現出するように、現世に誕生する。

数式についてはそんな感じを抱いている。

数式が望むか望まないかなんて正直知る由もないけれど、この話は「数学が"発明する"ものなのか、"発見するもの"なのか」という議論にも似ている気がする。

参考

www.youtube.com

【中古】 フランケンシュタイン / メアリー シェリー, 高田 勲, 加藤 まさし / 講談社 [新書]【メール便送料無料】【あす楽対応】

ただしい人類滅亡計画　反出生主義をめぐる物語 [ 品田 遊 ]