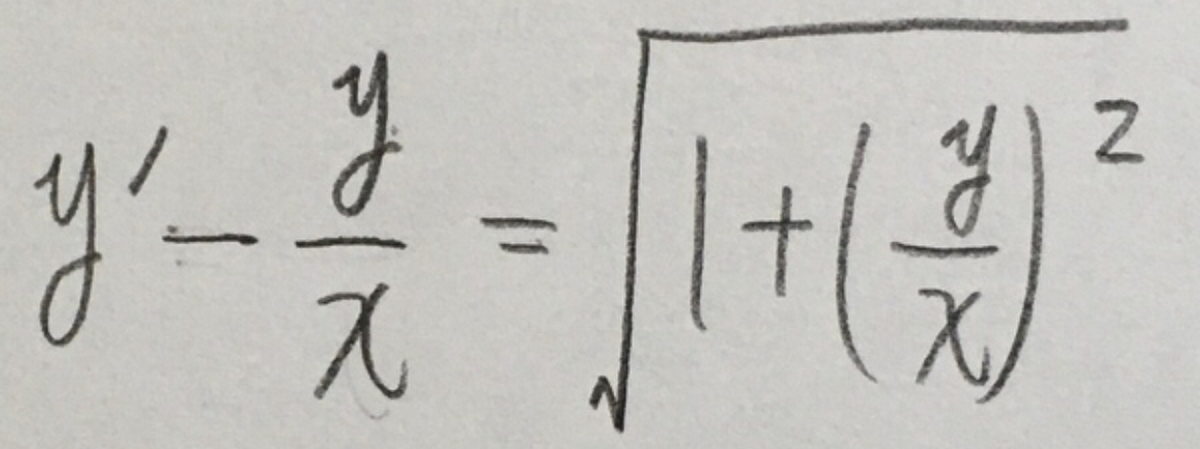質問
次の常微分方程式を解いて頂きたいです。よろしくお願いします。 - Yahoo!知恵袋
回答
まずは特徴的な y/x = u と置換しましょう。
ux = y なのでxについて微分して、
u'x + u = y'
よって与式を書き換えると、
(u'x + u) - u = √(1 + u²)
u'x = √(1 + u²)
u'/√(1 + u²) = 1/x
両辺を積分すると、よく出題されるパターンが現れて、
∫ du/√(1 + u²) = ∫dx/x = log|x| +C
= ∫dθ/cos(θ)
= (1/2)log( |1+sin(θ)| / |1-+sin(θ)| )
= log( (1sin(θ)+1))/cos(θ) )
= log( tan(θ) + 1/cos(θ) )
= log( u + √(1 + u²) )
よって、
u + √(1 + u²) = A e^x (A = Const.)
y/x + √(1 + (y/x)² ) = A e^x
y + √(x² + y²) = A x e^x
結果までの大まかな計算のながれはこんな感じですね。
参考になれば幸いです。
(回答ココマデ)